Problem Sets for Math 111

Lesson1: Points & Coordinates

1.     What are the coordinates of the points on the graph

2.     Draw Points at 7,2, and 3,5.

3.     What is the distance between:

7,2 and 3,2

3,5 and 3,2

7,2 and 3,5

4.     Draw points at: -5,8 8,-4 -7,-6 What is the slope of the line between: every pair of points.

5.     section 1.2 pages 22-23 ex. 1,2,5,6,7,8

6.      section 1.2 pages 22 ex. 21-38

Lesson 2: Functions

Fuel Efficiency

The United States federal highway Administration collects data on domestic motor fuel consumption. The table below lists the average fuel efficiency for cars in the U.S. measured in miles per gallon.

1.     Explain why the efficiency is a function of the year (why is year the independent variable).

2.     If F(year) is the fuel efficiency function:

3.     F(1985) = ?

4.     F(1992) = ?

5.     F(?) = 18.20

6.     F(?) = 21.69

7.     The empirical function describes just the data that is collected but does not consider the values that were not presented. What is the domain and range of the empirical fuel efficiency function?

8.     The actual function is the values that could have been measured even if no measure was taken. What do you think is the domain and range of the actual function? Why?

9.      Functions and Tables: Text Section 1.1 page 7-10 ex 8,9,23,24,31,32

10.    Functions and Graphs: Text Section 1.1 pages 7-10 ex. 10,11,12,13,19,20,25,28

11.    Word Problems for Functions: Text Section 1.1 pages 7-10 ex. 21,22,33,34

Lesson 3: Slopes

Driving Excitement

As you drive, your friend times how long it takes you to cover miles; he produces this table for you which you find quite distracting:

 

(r)

(s)

(t)

Minutes

2

8

10

Miles

1

4

5

1.     Write these numbers as ordered pairs with the minutes as the independent variable.

2.     On your graph paper, graph these pairs. How do you set up the axes? Do the three points line up?

3.     What are the slopes between all three points: r&s, s&t, and r&t?

4.     Draw the line through the three points. Can you find an equation for this line?

5.     How much time does it take to go 4 miles? 3 miles? 6 miles?

6.     How far can the car go after 2 minutes? 4 minutes? 9 minutes?

7.     Calculating Slope: Section 1.2 pages 15-18 ex. 1,2,15,16,18,19

8.     Slope from tables: Section 1.2 pages 15-18 ex.3,4,21,25,26

Lesson 4: Linear Functions

Part 1: Algebraically

  1. Find the intercepts of the line through these points with the specified slopes:

 

Point

Slope

(2,6)

-3

(3,-5)

-2

(6,7)

2

(6,8)

1/3
  1. Find the slope and intercepts of the line through these pairs of points:

Point 1

Point 2

(-1,1)

(3,9)

(2,6)

(5,3)

(6,8)

(-2,4)

(3,-5)

(-1,7)

(6,7)

(2,7)

 

1.     Linear Functions from tables: Section 1.3 page 25-27 ex 1,2,3,4,5,6,13,17,22,24,25

2.      Linear Function Word Problems: Section 1.3 pages 26-27 ex. 14,15,16,19,20,21,26,27,28

3.      Linear Functions from Points: Section 1.4 page 33 ex.16,17,18,19,20,21,22,23

4.      Linear Functions from Tables: Section 1.4 page 33 ex. 24,25,26,27

5.      Linear Function Word Problems: Section 1.4 pg 34-36 prob 38,39,40,41,42,47,48,49

6.     Freezing is 32 degrees Fahrenheit but 0 degrees Celsius. Boiling is 212 degrees Farenheight but 100 degrees Celsius. What is the Formula to translate Celsius to Farenheight? What is the Formula to translate Farenheight to Celsius? Why do we care?

Lesson 5: Linear Intersections

Intersect Algebraically and graphically these lines:

Intersect Algebraically and graphically these lines:

1.      y=2x+3  and y=3x+6

2.      y=2x-3 and y= -x+3

3.      slope 2 through (2,6)  and  linethrough (3,2) and (7,6)

4.      y= -2x+5  and  slope -4 through (3,5)

5.      y = ½x+3 and  slope 1 through (-2,3)

6.     Linear Intersection Word Problems: Section 1.5 page 43 ex. 19,20

7.     At the concert, you can sell 6 copies of your poster at $100 and 96 copies at $10 a piece. If you have time to make 42 copies before the concert then how much should you charge to sell all of them? If you charged $1 more would you make more money?

8.      

a.      If you charge $5 for a chicken you’ll sell 500 chickens but if you charge $4 for a chicken you’ll sell 800 chickens.  What is the linear demand function for chickens.

b.     You can get 400 chickens for $1.75 but the next 600 are  $2 (more expensive supplier).  What is the supply function for chickens?

c.      What is the equilibrium price for chickens?  What is the equilibrium demand?

9.      

a.      If you charge $1 for a quarter pound burger you’ll sell 5000 burgers but if you charge $0.75 for a quarter pound burger you’ll sell 8000 burgers.  What is the linear demand function for burgers.

b.     You can get 1 ton (2000 pounds of burger meat) for $1000 but the next ton is $1500 (more expensive supplier) (two tons will thus cost $2500, what will each ton cost?).  What is the supply function for burgers

c.      From a ton of burger meat you can make 8000 quarter pounders.What is the equilibrium price for burgers?  What is the equilibrium demand?

10.   

a.      You can sell 1000 doughnuts at $1.50 a piece but if you charge $1.75 you will sell 750.  What is the demand function for donuts.

b.     The cheapest bakery supplier will supply dough and fillings for 200 doughnuts at a price of $0.35 a doughnut (total price $70).  The next cheapest can supply 300 doughnuts at a price of $0.50 a doughnut.  How much does it cost in total to supply dough and fillings for 500 doughnuts?  How much per doughnut?  What is the supply function for doughnuts?

c.      What is the equilibrium price for doughnuts?  What is the equilibrium demand?

Lesson 6: Quadratics

1.     Quadratic Algebra Problems Section 3.2 pages 115-116 ex. 1,2,3,4,5,6,26,27,

2.     Quadratic Word Problems Section 3.1 pages 116 ex. 30,31

3.     If you charge $20 your store sells 500 crystals a year. When you raise the price by $1 you sell 10 less, if you lower the price by $1 you sell 10 more. To produce the crystals costs $1000 fixed costs and $5 of materials for each crystal. How much do you charge to maximize revenue (total money the store collects)? How do you charge to maximize your profits (revenue-manufacturing costs)? Whats the maximum price that earns you more than $5000?

4.     You can sell 30 paintings at $20 and reducing the price by $2 allows you to sell 10 more paintings.  You can get supplies for 15 paintings from one supplier at $6 a painting.  You can get supplies from another supplier for 30 paintings at $7.50 a painting.  What should you charge to maximize profit?

Lesson 7: Quadratic Intersections

1. Find the intersection points between these curves - Graphically and Algebraically:

y=x2-4x+7

y=x+3

y=x2-4x+7

y=-x+5

y=x2-4x+7

y=x2-2x+1

y=x2-4x+7

y=x2-12x+41

y=x2-2x+1

y=-x2+10x-15

y=x2-2x+1

y=-x2+6x+1

Lesson 8: Finding Quadratics

 

1. find the quadratic through these triples:  (See worksheet above).

1,2

2,3

3,6

-1,2

2,-1

3,-6

1,5

-2,-3

3,6

1,-2

-2,4

3,-6

Lesson 9: Rational Functions

1.      Rational Function Formulae Problems: Section 11.5 page 465 ex 1,2,3,4,5,6,7,8

2.      Find the asymptotes of

1.     

 

2.     

 

3.     

 

4.     

 

5.     

 

6.     

 

Lesson 10: Composition and Inverse of Functions

1.      Function Composition Table Problems: Section 10.1 page 401-404 ex.6,7,28,29,30,55

2.      Function Composition Formulae Problems: Section 10.1 page 401-404 ex.1,2,3,9,9,10,11,12,13,62

3.      Function Composition Word Problems: Section 10.1 pages 404 ex. 56

4.      Function Inverse Formula Problems Section 10.2 page 411-414 ex.15,16,17,18,19,20,21,22,23,24,25,26

5.      Function Inverse Word Problems: 35,36,37,38

6.     ,  what is ,,,

7.     ,  what is ,,,

8.      Find the inverse of:

1.     

2.     

3.     

4.     

5.     

9.     ,  what is , show , what is , show

10.  ,  what is , show , what is , show

11.  Demand functions tell you how much of a product such as cheese you can sell at a specified price. They have negative slopes, why? Interpret the inverse function of demand. Discuss who might want to know it. What will its slope be? Why?

Lesson 11: Exponential Functions

1.     Calculate: 34, (1/3)4, (2/3)4, 3-4, (1/3)-4, (2/3)-4

2.     Express as simply as possible: (a2)(a3), (a3)(a-2), a-2b-2, a3b-3, (d2)3,d23, (n-3k6)2/3

3.      Exponential Function Problems: Section 4.1 page136-137. ex. 18,21,23,24,25,26,27

4.      Exponential Word Problems: Section 4.1 pages 136-138  ex. 19,20,29,30,31,32,33,35,36,37,38,39,40,41,45,46,47,48

5.     Compound Interest Problems: Section 4.4 page.156 ex. 1,2,3,4,5,6,7,8,9,10,11,12,13,14

6.     Compound Interst Word Problems: Section 4.4 pages 156 ex. 15,16,17,18,19,20,21,22 
Section 4.5 page 165 ex. 30,31,32,33,36,37,38,39,40,45,46

Lesson 12: Logarithms

1.     Logarithm Algebra Problems Section 5.1 page 184 ex 1,2,3,4,5,6,19,20

2.     Logarithm Equation problem: Section 5.1 page 187 ex 34,35,37,38,39,40

3.      

a.      If you charge $5 for a chicken you’ll sell 500 chickens but if you charge $4 for a chicken you’ll sell 800 chickens.  What is the exponential  demand function for chickens.

b.     You can get 400 chickens for $1.75 but the next 600 are  $2 (more expensive supplier).  What is the exponential supply function for chickens?

c.      What is the equilibrium price for chickens?  What is the equilibrium demand?

4.       

a.      If you charge $1 for a quarter pound burger you’ll sell 5000 burgers but if you charge $0.75 for a quarter pound burger you’ll sell 8000 burgers.  What is the exponential demand function for burgers.

b.     You can get 1 ton (2000 pounds of burger meat) for $1000 but the next ton is $1500 (more expensive supplier) (two tons will thus cost $2500, what will each ton cost?).  What is the exponential supply function for burgers

c.      From a ton of burger meat you can make 8000 quarter pounders.What is the equilibrium price for burgers?  What is the equilibrium demand?

5.       

a.      You can sell 1000 doughnuts at $1.50 a piece but if you charge $1.75 you will sell 750.  What is the exponential demand function for donuts.

b.     The cheapest bakery supplier will supply dough and fillings for 200 doughnuts at a price of $0.35 a doughnut (total price $70).  The next cheapest can supply 300 doughnuts at a price of $0.50 a doughnut.  How much does it cost in total to supply dough and fillings for 500 doughnuts?  How much per doughnut?  What is the exponential supply function for doughnuts?

c.      What is the equilibrium price for doughnuts?  What is the equilibrium demand?

Lesson 13: Trigonometry Definitions

1.     How many radians is 60o, 30o, 15o, 135o, 400o

2.     Show where each of these lie on the unit circle.

3.     How many degrees in p radians, p/4 radians, 3p/8 radians, 1 radian, 7 radians.

4.     Show approximately where each of these lie on the unit circle.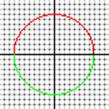

5.     Radians Degrees Problems Section 8.1 pages 322-323 ex. 1,2,3,4,5,6,7,8,9,10,11,12

6.     What is the sin, cos and tan of the angle that the line y= x makes with the line y=0.

7.     What is the sin, cos and tan of the angle that the line y= 2x makes with the line y=0.

8.     What is the sin, cos and tan of the angle that the line y= ½x makes with the line y=0.

9.     What is the sin, cos and tan of the angle that the line y= -x makes with the line y=0.

10.  What is the sin, cos and tan of the angle that the line y= -2x makes with the line y=0.

11.  What is the sin, cos and tan of the angle that the line y= -2x makes with the line x=0.

12.  What is the sin, cos and tan of the angle that the line y= x makes with the line x=0.

13.  What is the sin, cos and tan of the angle that the line y= ½x makes with the line x=0.

Lesson 14: Trigonometry Functions

1.     Build these tables:

 

-p /2

-p /4

0

p/4

p/2

3p /4

p

5p /4

3p /2

7p /4

2p

Sin(x)

.

.

.

.

.

.

.

.

.

.

.

Cos(x)

.

.

.

.

.

.

.

.

.

.

.

2sin(x)

.

.

.

.

.

.

.

.

.

.

.

Sin(2x)

.

.

.

.

.

.

.

.

.

.

.

-cos(x)

.

.

.

.

.

.

.

.

.

.

.

2.     Use the tables to graph sin(x), cos(x), 2sin(x), sin(2x), - cos(x).

3.     Give the amplitude, frequency, and altitude for each of the functions below

4.     (each x box is p/4 radians):
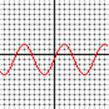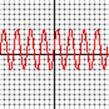(a) (b) (c)  

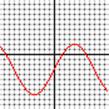
Graph each of these functions:

5.     · sin(2x )

6.     · -cos(-x)

7.     · 3cos(x+p ) +2

8.     · 2sin(2x +p /2)-2

9.      Trigonometric function graphing Problems: Section 8.2 page 330-333 ex.1,2,3,4,9,10,11,12,13,14,17,18,19,20

Lesson 15: Trigonometric Inverse

1.      Section 8.4 page 347-349 ex. 1,2,3,4,5,6

 

© David B. Sher 2001